CNN 对模式分类非常适合,其最初是为识别二维形状而特殊设计的,这种二维形状对平移、比例缩放、倾斜或其他形式对变形有高度不变性。
图像识别/分类
图片识别/分类的一般过程:detect -> align -> represent -> classify。具体到 CNN 就是检测到图片的位置,剪出来对齐,表达特征,对若干层进行不同的卷积、pooling,最后全连接网络做分类。
传统模型:
Fixed features + unsupervised mid-level features + simple classifier
神经网络:
Low-level features -> Mid-level features -> High-level features -> trainable classifier
李飞飞的 ImageNet 比赛,在 2012 年之前,经典做法是人工选一些原始特征出来(SIFT, Hog, Harr, etc.),再稍加变换,可能用到一些聚类的算法,做一些中等级别的特征,然后给某个分类器做识别,一般就是 SVM。这种方法每一步都会损失数据,到最后可能就达不到很好的分类效果。
注: 把图像像素看成 words of bags,不同的原始图像可能分别是 M1*N, M2*N, M3*N 等等的 vectors,通过 K-means 的聚类聚比如说 1000 个类,就能把原来的 vectors 转化成长度为 1000 的直方图,也就形成中等级别的特征,维度就一样了,然后再选一个分类器。
2012 年第一次用了 CNN,正确率提高了 10%,人们意识到深度学习可能是图像识别非常有效的方式。与传统模型不同的是特征是自动选择的。
深度学习现在看来还可能是过冗余的,可以很多改进空间,如果能把 100M -> 100K 的参数,就可以不用离线训练,也可以放到 App 中了。
卷积神经网络
传统的神经网络都是采用全连接的方式,即输入层到隐藏层的神经元都是全部连接的,这样做将导致参数量巨大,使得网络训练耗时甚至难以训练,而 CNN 则通过局部连接、权值共享等方法避免了这一困难。
特点
通过局部连接和权值共享减少了神经网络需要训练的参数的个数。
- 局部连接
- 权值共享(每个 feature map 共享参数)
- 池化
一般架构
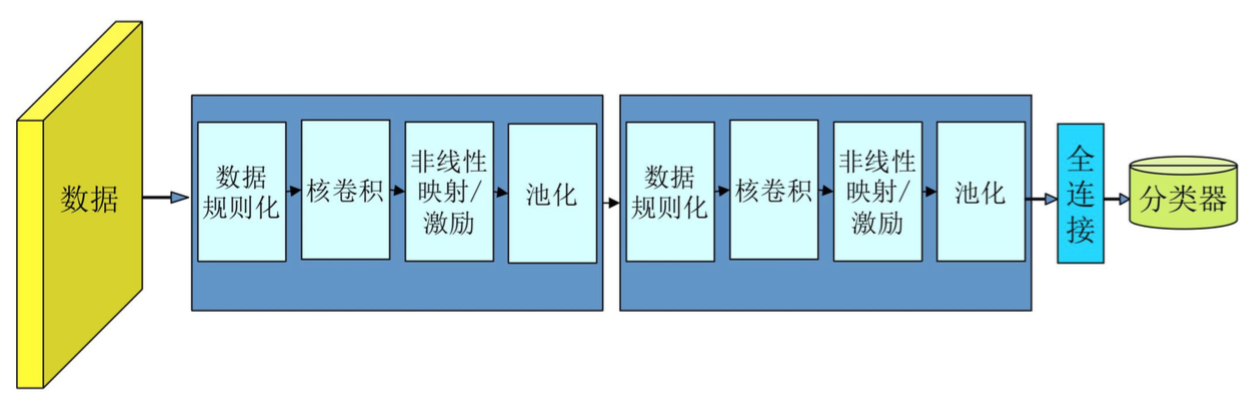
可能有多个卷积层或多个输出层,某些卷积层不跟着 pooling 也是可以的。
卷积层(Convolutional Layer)
卷积层是卷积神经网络基本结构,它由多个卷积核组合形成,每个卷积核同输入数据做卷积运算,形成新的特征图(feature map),也就是,有几个卷积核,就有几个特征图。
比如说一张 32*32 的 RGB 图片,做卷积,一张图片就能理解。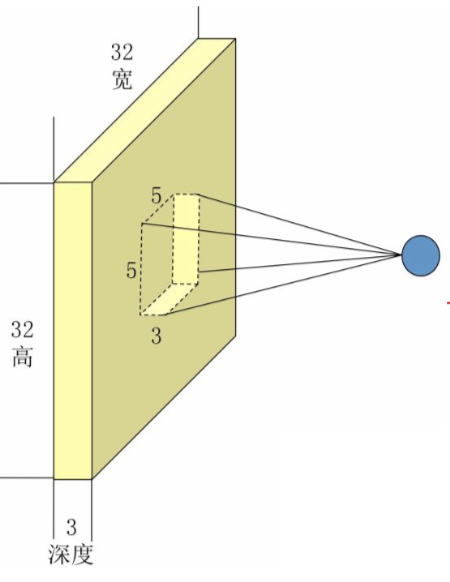
Input volume: 32*32*3 Receptive fields: 5*5, stride 3 Number of neurons: 5 Output volume: (32-5)/3+1=10, -> 10*10*5 Weights for each of 10*10*5 neurons: 5*5*3=75
这其中,卷积核的 大小(size) 是由用户定义的,而 深度(或者说厚度),是由输入数据定义的,一维数据就用一维卷积核,RGB 图片就是三维卷积核。
卷积核的 数目(kernel number),常见参数有 64,128,256,为了使 GPU 并行更加高效。
每一个神经元从上一层的局部接受域得到输入,提取局部特征,每个局部特征相对于其他特征的位置被近似保留下来,原本的精确位置就没那么重要了。每一个计算层都由多个 feature map 组成,每个 feature map 都是平面形式的,平面中单独的神经元在约束下共享相同的权值集。这种结构约束具有平移不变性(强迫 feature map 的执行使用具有小尺度核的卷积,再接着使用一个 sigmoid 函数),另外,权值共享也可以实现自由参数数量的缩减。
卷积核的“矩阵”值,就是卷积神经网络的参数,卷积核的初值,通常随机生成,然后通过反向传播更新。随机生成可以通过高斯分布生成。一个问题:
卷积核初值完全一样好不好?
不好!如果初值完全一样,那么反向梯度改变的量也差不多,整体就没有变化性,没有多样性。
padding & stride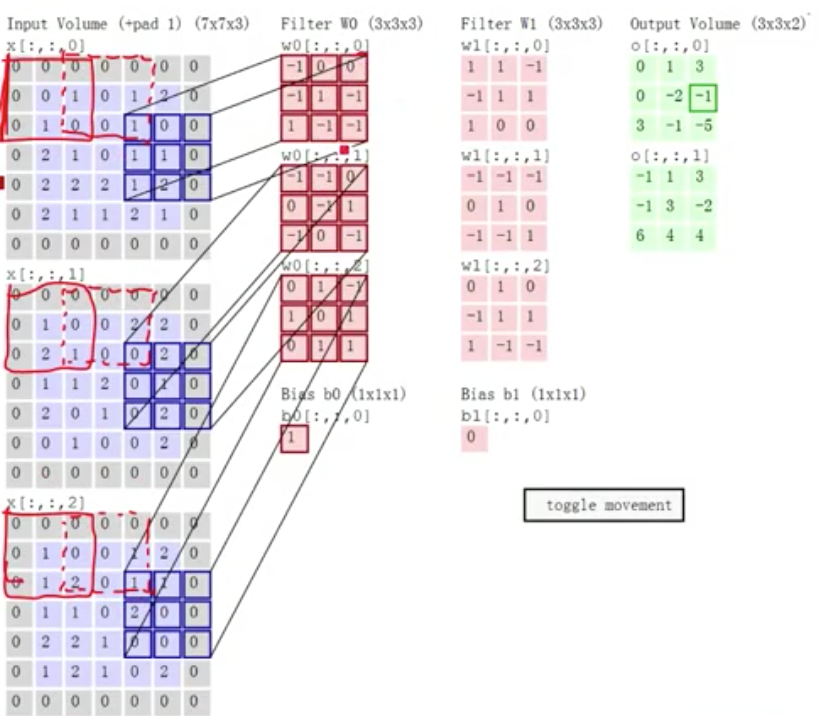
padding 也就是边界扩充,在卷积计算过程中,为了允许边界上的数据也能作为中心参与卷积计算,将边界假装延伸,目的是为了确保卷积后特征图尺度一致。卷积核的宽度为 2i+1,添加 pad 的宽度就为 i。如上图,5*5 的图,卷积核 3*3,取 padding=1,对原始数据上下左右各补 1,可能会有偏移量,就相乘相加再加上偏移值。
步长(stride)是对输入特征图的扫描间隔,因为相邻的卷积窗口传达的信息可能会差不多,所以跳着取,提高效率。
权值设置:
可以对所有权值做先验处理,按高斯分布做随机处理,然后梯度下降调整权值。
功能层
卷积神经网络还需要一些额外功能:
- 非线性激励: 卷积是线性运算,需要增加非线性描述能力
- 降维: 特征图稀疏,需要减少数据运算量,保持精度,如做一个 pooling
- 归一化: 特征的 scale 保持一致,比如说映射到 [0,1] 之间
- 区域分割: 不同区域进行独立学习
- 区域融合: 对分开的区域合并,方便信息融合
- 增维: 增加图片生成或探测任务中的空间信息
非线性激励层(None-linear activation layer)
如 ReLU 函数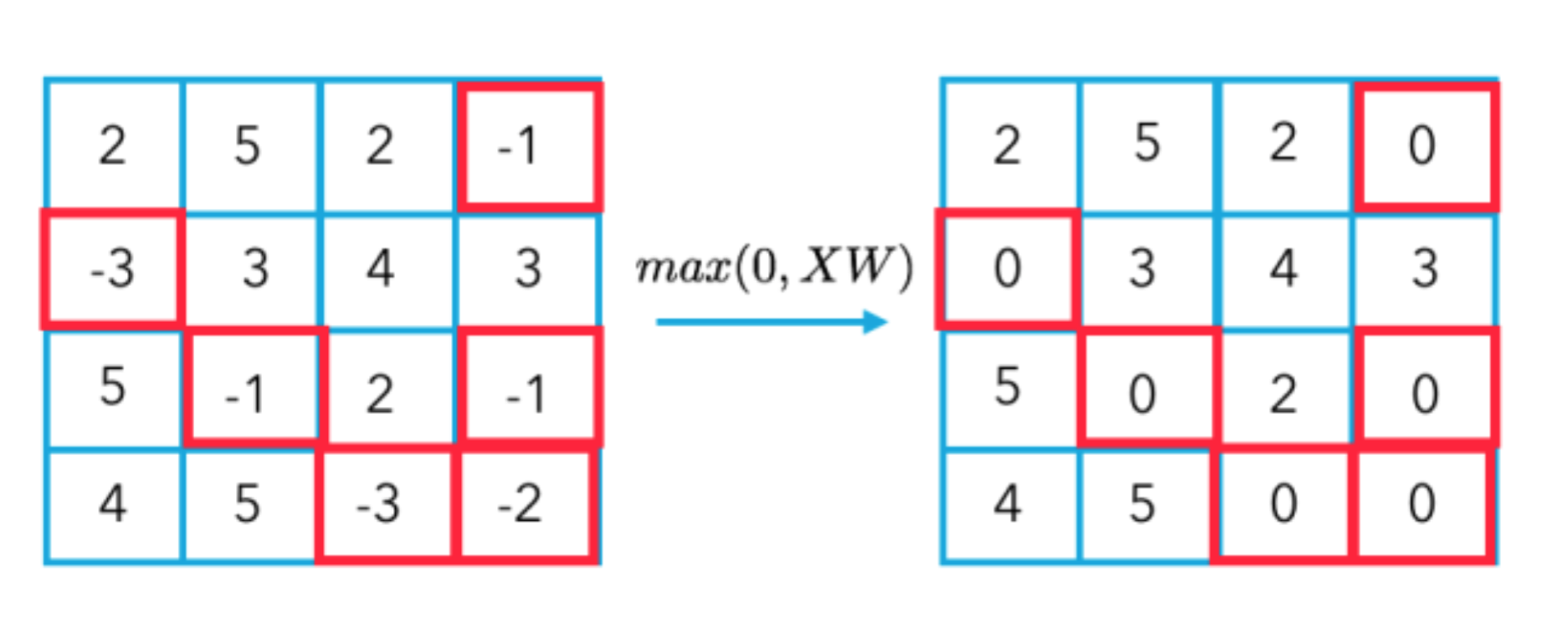
更多见 神经网络-从线性到非线性
池化层(Pooling layer)
每个卷积层跟着一个实现局部平均和子抽样的计算层,能达到降维的目的,由此 feature map 的分辨率降低。这种操作可以使 feature map 的输出对平移和其他形式的变形的敏感度下降。一张图解释下 2*2 的 max-pooling。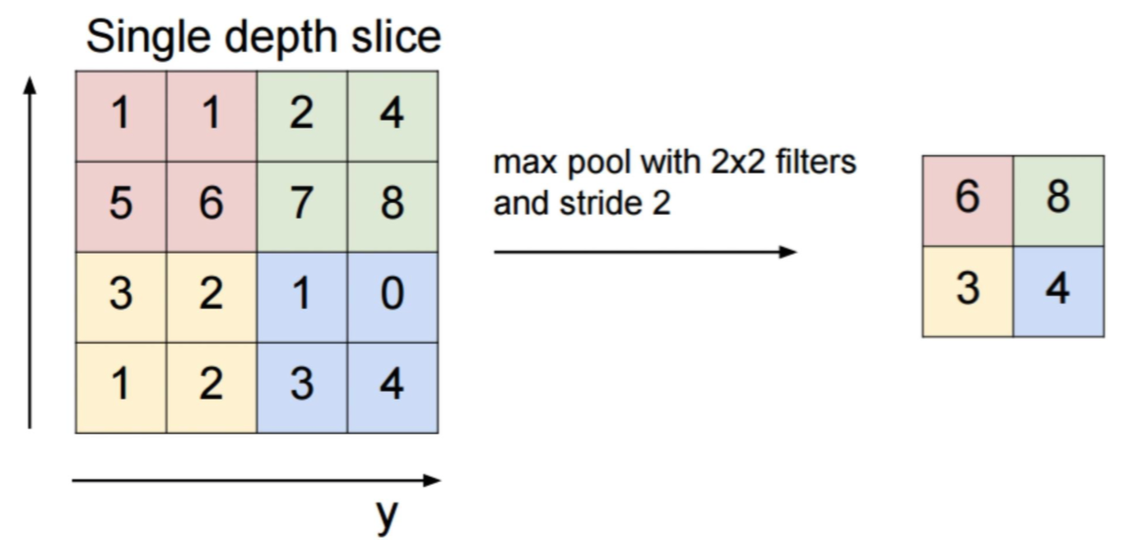
这样 M*M 的图像就成了 M/2 * M/2 的图像。当然还有 min-pooling 和 avg-pooling。
作用:
- 降低输出规模
- 增加可解释性
- 避免丢失过多信息
归一化层(Normalization layer)
如 批量归一化(Batch Normalization, BN),原因是特征数的 scale 不一致,好处是可以加速训练,提高精度。
还有 近邻归一化(Local Response Normalization),与 BN 不同的是,BN 依据 mini batch 的数据,而 LRN 仅需要自身,BN 训练中有学习参数,而 LRN 并没有。
$$x_i={x_i \over (k+(\alpha \sum_jx^2_j))^\beta}$$
切分层(Slice layer)
在某些应用中,希望独立对某些区域单独学习,比如说人脸识别,可以眼睛一套参数,耳朵一套参数。。好处是可以学习多套参数,得到更强的特征描述能力。
融合层(Merge layer)
对独立进行特征学习的分支进行融合,来构建高效而精简的特征组合。
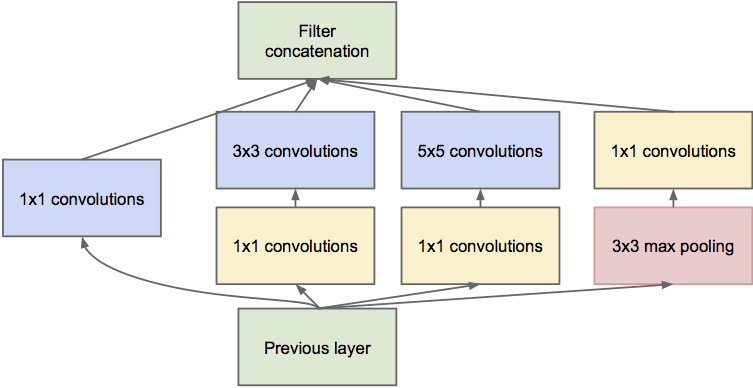
可以用 级连(concatenation) 的方法,其实也就是不同输入网络特征的简单叠加,比如说首尾相接。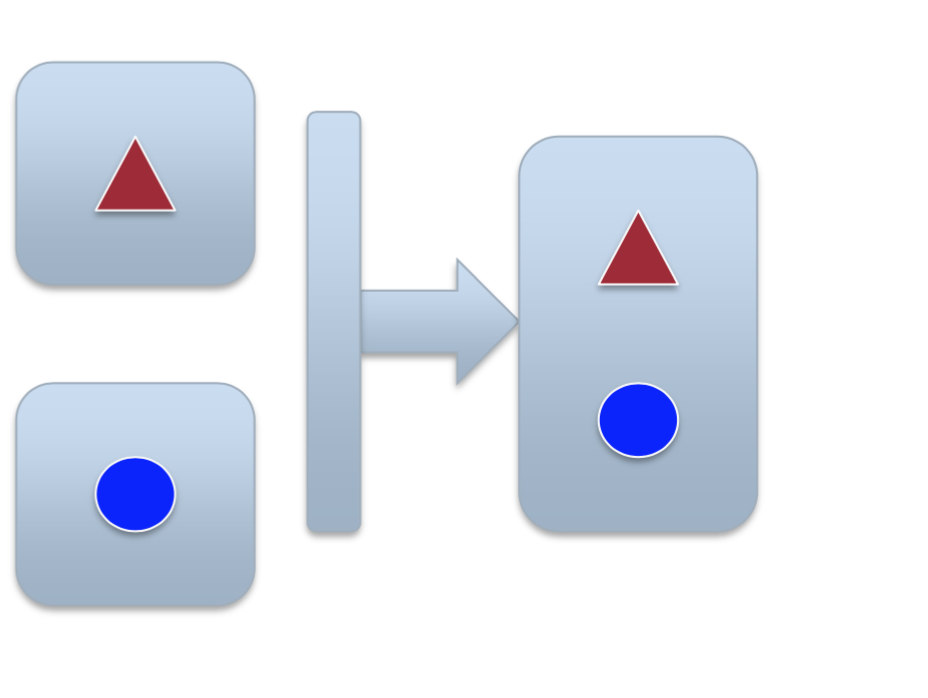
也可以是合并,或者说运算的融合,对形状一致的特征曾,通过 +, -, x, max, conv 等原酸,形成形状相同的输出,如微软的残差网络。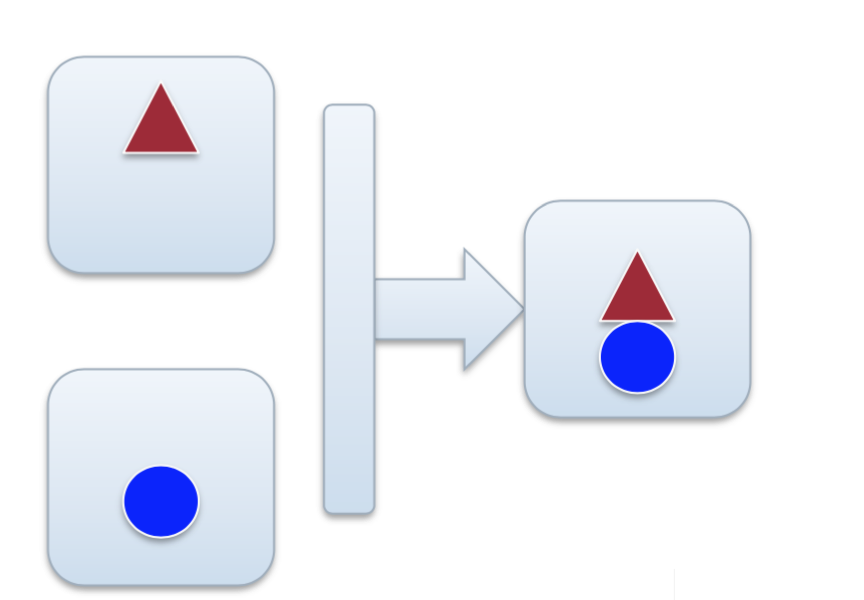
全连接层及全卷积网络
最后的输出一般是连一层全连接层(fully connected layer),相当于 softmax 回归。当然其实也可以不连,像 FCN(全卷积网络)。
卷积层 的操作可以把 kernel 作用于输入的不同区域然后产生对应的特征图,也因此给定一个卷积层,并不要求输入是固定大小的。而 全连接层 的操作实际上是把输入拉成一个一维的向量,然后对这个一维向量进行点乘,这要求输入是固定大小的。这有的时候是很不合理的,如下图,如果要把红框的塔输入网络,就会产生图片变形。
如何网络接受任意的输入?
把全连接层变成卷积层,这就是所谓的卷积化。这里需要证明卷积化的等价性。直观上理解,卷积跟全连接都是一个点乘的操作,区别在于卷积是作用在一个局部的区域,而全连接是对于整个输入而言,那么只要把卷积作用的区域扩大为整个输入,那就变成全连接了。所以我们只需要把卷积核变成跟输入的一个map的大小一样就可以了,这样的话就相当于使得卷积跟全连接层的参数一样多。举个例子,比如 AlexNet,fc6 的输入是 256x6x6,那么这时候只需要把 fc6 变成是卷积核为6x6的卷积层就好了。
与传统神经网络相比,CNN 参数和计算量更多还是更少了?
参数变少了,因为都使用一套参数,而计算量却是变大了,因为卷积窗口要滑到不同的地方,进行计算、合并等操作。
优化
提高泛化能力(减少 overfit)
- 增加神经网络层数。使用卷积层极大地减小了全连接层中的参数的数目,使学习的问题更容易
- 使用更多强有力的规范化技术(尤其是 dropout 和 regularization)来减小过度拟合
- 使用修正线性单元而不是 S 型神经元,来加速训练-依据经验,通常是3-5倍
- 使用 GPU 来计算
- 利用充分大的数据集,避免过拟合
- 使用正确的代价函数,避免学习减速
- 使用好的权重初始化,避免因为神经元饱和引起的学习减速

